Cadena de Markov (MC)
La segunda acepción de la RAE nos dice que una secuencia “es una sucesión de cosas que guardan entre sí cierta relación”. En el mundo real podemos encontrar innumerables ejemplos que se ajustan a esta definición. Por ejemplo, en aplicaciónes de transformación de audio a texto y visceverza, pronóstico del clima, en el control de robots o procesamiento de video, etc. En ese sentido, es importante poder abstraer modelos matemáticos que nos permitan estudiar mejor estos procesos.

Sistema secuencial de sugerencia de texto
El problema de la dimensionalidad
El siguiente grafo o propiamente dicho: Modelo Gráfico probabilistico (PGM) representa un sistema secuencial de longitud de secuencia $$T=4$$.
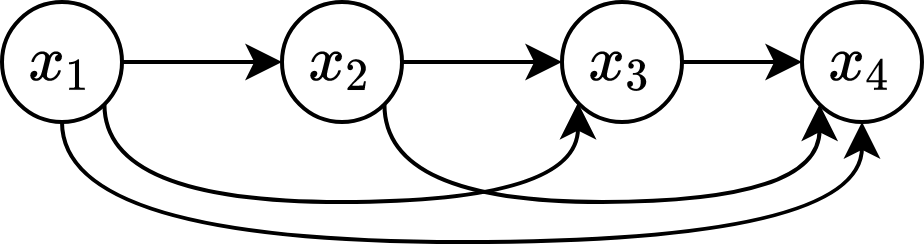
Modelo de un sistema secuencial sin ninguna asumpción
Siguiendo la regla de la cadena para un modelo de longitud arbitraria $$T$$ se obtiene la probabilidad de dicho evento.
$$p(x_{1:T}) = p(x_1)p(x_2|x_1)p(x_3|x_2,x_1)\cdots p(x_T|x_{1:T-1})$$
El número de parametros para resolver este problema es del orden de $$O(M^T)$$, siendo M el número de estados y T el orden de la secuencia. De aquí que el número de parámetros se incremente exponencialmente a medida que crecen los estados y el orden de la secuencia, lo que hace impráctico este tipo de soluciones para problemas que empiezen a crecer en complejidad.
Markov Chain y la asumpción de independencia
En el ejemplo anterior vimos que un modelo sin ninguna asumpción puede requerir una cantidad muy grande de parámetros. Markov Chain es una forma en como podemos plasmar un modelo secuencial de una forma sencilla bajo la asumpción de que la probabilidad que ocurra un estado $$x_t$$ en un tiempo determinado $$t$$ únicamente depende de lo que ocurre un instante anterior $$x_{t-1}$$, como se puede ver en la ecuación y grafo siguiente. Bajo esta asumpción se reduce el número de parámetros a $$O(K^2)$$, como veremos más adelante esto es: una matriz cuadrada de dimensión 2.
$$p(x_t|x_{t-1})$$

Modelo Gráfico Probabilistico de una Cadena de Markov, note que cada estado depende únicamente del estado anterior a excepción del primer estado.
Por lo que podemos escribir la probabilidad de un evento (secuencia de estádos) $$x_1, x_2, x_3, \cdots,x_T$$ que sigue un Proceso Markoviano tiene la forma:
$$p(x_{1:T}) = p(x_1)\prod_{t=2}^T p(x_t|x_{t-1})$$
Donde $$p(x_1)$$ es la probabilidad de que dicho evento empieze en el estado $$x_1$$.
Nótese que la asumpción de Markov de que el estado siguiente solo depende del estado actual únicamente es cierto cuando se conoce el estado actual. En otras palabras, “el estado siguiente es independiente de los estádos anteriores dado que se conoce el estado actual”, es decir $$x_{t+1} \perp x_{1:t-1} | x_t$$.
Esto puede ser una asumpción fuerte para ciertas aplicaciones que implica que en cada estado conocemos toda la información necesaria para predecir el estado siguiente. Por ejemplo, consideremos que estamos intentando obtener la posición de un robot mediante una cámara. Definimos que el estado actual son los píxeles del frame actual $$x_t = F_t$$, se puede intuir que este sistema no cumpliría con la propiedad de Markov, ya que los píxeles de un único frame no nos informa de hacia donde se mueve el objeto por lo que no se podría saber cual es la posición en $$t+1$$.
Una solución para escenarios donde no se cumple la propiedad de Markov es utilizar Cadenas de Markov de órdenes mayores a uno. Por ejemplo una cadena de Markov de segundo orden tiene la siguiente propiedad: $$p(x_t|x_{t-1}, x_{t-2})$$, es decir: el estado actual depende de los 2 estados anteriores. En ese sentido, uno podría pensar aumentar el orden de la cadena, pero nótese que el caso extremo es el presentado en el primer ejemplo, donde se tiene $$O(M^K)$$ parámetros.
Existen otros métodos como los Modelos Ocultos de Markov (HMM), que estan diseñados para solucionar estas dependencias o correlaciones con los estados anteriores, o cuando las entradas son ruidosas. Esto lo veremos en otro post.
Referencias
[1] Kevin P. Murphy. Machine Learning: A probabilistic Perspective, First edition, 2012.
Author Erick Tornero
LastMod 2020-03-21